Suche Home Einstellungen Anmelden Hilfe

Aufgabe zur Minimierung

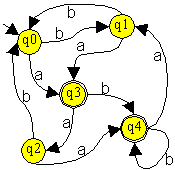Der Automat M = ({q0,...,q5},{a,b},,q0,{q3,q4}), wobei die Übergänge am Graphen abgelesen werden können, ist zu minimieren.         Minimiert sieht der entstehende Automat M' folgendermaßen aus: 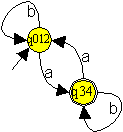Nun ist auch einfach ablesbar, welche Sprache der Automat akzeptiert.

Minimieren Sie den nebenstehenden Automaten M! (0. Schritt: Die Graphdarstellung des Automaten ist vollständig, es müssen keine weiteren Übergänge beachtet werden.) 1. Schritt: Aufbau der Matrix 1   2     3       4         0 1 2 3 2. Schritt: Markieren aller Paare, die nur einen Endzustand enthalten. Das sind alle Paare, die entweder q3 oder q4 enthalten. 1   2     3 * * * 4 * * *   0 1 2 3 3. Schritt: Berechnen von {(q,a), (q',a)} (für jedes verbleibende Zustandspaar und jedes Eingabesymbol) und überprüfen, ob das Ergebnispaar markiert ist. a b {q0,q1} {q3} {q0,q1} {q0,q2} {q3,q4} {q0,q1} {q1,q2} {q3,q4} {q0} {q3,q4} {q1,q2} {q4} Bei der Berechnung entstehen keine bereits markierten Paare. Die obige Tabelle ist somit zugleich das Endergebnis. Äquivalent sind jeweils die Paare {q0,q1}, {q0,q2}, {q1,q2} und {q3,q4}. Die ersten drei führen zum Zustand {q0,q1,q2}

Schritt 3 1   2   3   4 Übersicht: Sprachklassen

Benutzer: Gast • Besitzer: senn • Zuletzt geändert am: