|
Eine unendliche Menge M heißt abzählbar
unendlich (kurz: abzählbar), wenn es
eine bijektive Abbildung f: IN-->M gibt (oder – was gleichwertig
ist – wenn es eine
bijektive Abbildung g: M-->IN gibt). f nennt man Abzählung.
Ist M unendlich, aber nicht
abzählbar, so heißt M überabzählbar.
Satz:
1) Jede unendliche Teilmenge einer abzählbaren Menge ist abzählbar.
2) Jede Obermenge einer überabzählbaren Menge ist überabzählbar.
Beweis:
1) Sei M eine abzählbare Menge und M'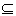 M
eine unendliche Teilmenge. Sei M
eine unendliche Teilmenge. Sei
f: IN-->M.eine Abzählung von M. Seien k0, k1,
k2, k3, ...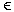 IN
diejenigen natürlichen Zahlen, für die
f(ki ) IN
diejenigen natürlichen Zahlen, für die
f(ki )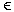 M'
gilt. Eine Abzählung f' von M' erhält man dann durch die Definition: M'
gilt. Eine Abzählung f' von M' erhält man dann durch die Definition:
f': IN-->M' mit f'(i)=f(ki ) für alle i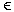 IN.
• IN.
•
Satz:
Die Menge aller Algorithmen ist abzählbar.
Beweis:
Die Menge aller Algorithmen ist eine Teilmenge von X* . Wegen o.g. Satz
brauchen wir
also nur zu zeigen, dass die Menge aller endlich langen Texte X* , die
man über dem
Alphabet X bilden kann, abzählbar ist.
Sei |X| die Anzahl der Elemente des Alphabets X. Die Elemente von X mögen
irgendwie
angeordnet sein, z.B. so:
X={'a',...,'z','A',...,'Z','0',...,'9',',',':',...,'-','+','à'}.
Sei
p: X-->{1,2,...,|X|}
eine totale Funktion, die jedem Zeichen x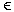 X
die Stelle zuordnet, an der es im Alphabet X
die Stelle zuordnet, an der es im Alphabet
X auftritt. Zum Beispiel gilt p('a')=1, p('z')=26, p('7')=60 usw.
Sei nun w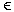 X* ein beliebiges
Wort. w hat eine endliche Länge |w|=n X* ein beliebiges
Wort. w hat eine endliche Länge |w|=n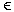 IN,
d.h. IN,
d.h.
w=x1 x2 x3 ...xn , xi
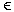 X für alle i X für alle i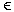 {1,...,n}. {1,...,n}.
x 1 ,...,x n sind die Zeichen, aus denen w aufgebaut ist. Dann definieren
wir folgende
Funktion:
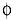 : X* -->IN durch : X* -->IN durch
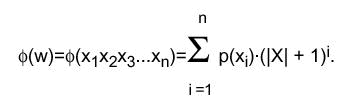
Speziell sei 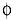 ( (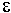 )=0.
Offensichtlich ordnet f jedem Wort aus X* genau eine Zahl zu. )=0.
Offensichtlich ordnet f jedem Wort aus X* genau eine Zahl zu. 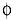 ist
ist
also eine totale Funktion. Wir behaupten: 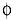 ist injektiv. Hierzu beachte man, dass stets
ist injektiv. Hierzu beachte man, dass stets 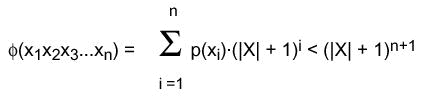
gilt. Man betrachte nun zwei beliebige Wörter v,w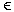 X*
. Wenn diese zwei Wörter v und w X*
. Wenn diese zwei Wörter v und w
verschiedene Länge besitzen, dann gilt wegen obiger Ungleichung sicher
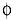 (w) (w)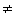 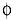 (v).
Sei (v).
Sei
daher |w|=|v|, also w=x1 x2 x3 ...xn
und v=y1 y2 y3 ...yn für
ein n>= 0. Weiterhin gelte
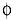 (w)= (w)=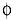 (v),
d.h.: (v),
d.h.:
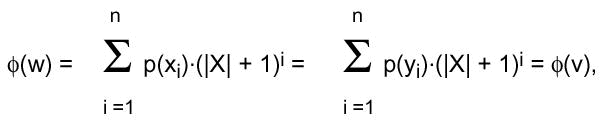
folglich:
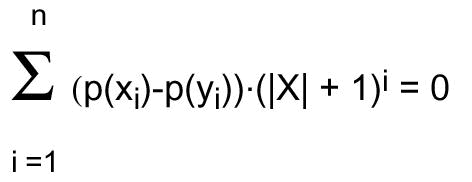
Dies kann aber nur zutreffen, wenn p(xi )-p(yi )=0
für alle i gilt. Da p bijektiv ist, müssen
also alle xi gleich den yi sein. Wir haben somit
gezeigt, daß für beliebige Wörter v und w
die Gleichheit 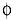 (w) = (w) =
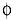 (v) nur gelten kann,
wenn v=w ist. Folglich ist (v) nur gelten kann,
wenn v=w ist. Folglich ist 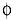 injektiv.
injektiv.
Wir betrachten nun 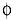 (X*
). Da X* eine unendliche Menge und (X*
). Da X* eine unendliche Menge und 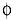 eine injektive Funktion ist,
eine injektive Funktion ist,
muß auch 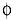 (X* )
eine unendliche Menge sein. Nach o.g. Satz ist jede unendliche Teilmenge (X* )
eine unendliche Menge sein. Nach o.g. Satz ist jede unendliche Teilmenge
von IN abzählbar unendlich, also auch 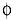 (X*
). Da (X*
). Da 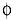 (X* ) gleichmächtig
zur Menge X* ist, (X* ) gleichmächtig
zur Menge X* ist,
folgt hieraus die Abzählbarkeit von X*. Somit ist auch die Menge
aller Algorithmen als
unendliche Teilmenge von X* abzählbar. •
|
 Übersicht: Sprachklassen
Übersicht: Sprachklassen