|
| |||||||||||
|
Andreas Ziehe und Klaus-Robert Müller, GMD Forschungszentrum
Informationstechnik GmbH
Die Extraktion von relevanten Informationen aus einem Gewirr von Umgebungsreizen (Signalen) stellt eine Herausforderung dar, die alle Lebewesen im Laufe ihrer Entwicklung zu meistern haben. Das Bestreben, auch Computer mit solchen Fähigkeiten auszustatten, ist Gegenstand einer faszinierenden neuen Forschungsrichtung - der Signalquellentrennung.
Das bekannteste Beispiel für eine solche Quellentrennung ist das sogenannte Cocktailparty-Problem. So bereitet es einem Menschen mit normalem Gehör in der Regel keine Probleme, sich mit einem Gesprächspartner auf einer Cocktailparty zu unterhalten und ihn zu verstehen, auch wenn viele andere Sprecher oder Störgeräusche in der unmittelbaren Umgebung vorhanden sind. Denn das Gehirn ist sehr gut in der Lage, unerwünschte Signale zu unterdrücken und erwünschte hervorzuheben.
Traditionelle technische Lösungen für das Cocktailparty-Problem arbeiten mit Frequenzfiltern. Um eine algorithmische Lösung für zu finden, muß man es zunächst mathematisch formalisieren. Im einfachsten Fall beispielsweise so: Über die Zeit t werden N verschiedene gemischte Mikrofonsignale xi(t) gemessen:
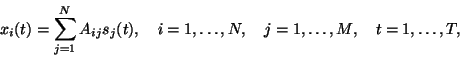
die sich jeweils aus einer linearen Mischung von M Originalsignalen sj(t) ergeben. Die entsprechende Spalte der Matrix Aij enthält dabei die Mischungsverhältnisse. Da weder Aij noch sj(t) bekannt sind (beide müssen geschätzt werden), wird dieses Problem auch als blinde Quellentrennung bezeichnet.
Algorithmen für derartige Probleme werden in der Arbeitsgruppe
IDA (intelligente Datenanalyse) am Forschungsinstitut für Rechnerarchitektur
und Softwaretechnik (FIRST) der GMD-Forschungszentrum Informationstechnik
GmbH, einer Forschungseinrichtung des Bundes, unter Gesichtspunkten wie
Trennungsleistung, Robustheit und Datenabhängigkeit analysiert und
weiterentwickelt.
Im Gegensatz zu den herkömmlichen Verfahren, die meist auf Frequenzfiltern
beruhen, nutzen diese neueren Algorithmen die gleichzeitige Aufzeichnung
von mehreren Mischsignalen, um durch Interferenz maximal unabhängige
Ausgabesignale ui zu erhalten, d.h., es ist das Ziel, die Abhängigkeiten
zwischen den einzelnen Mikrofonsignalen zu verringern und auf diese Weise
die Originalsignale zu rekonstruieren (s. Abb.).
In der oben definierten Terminologie gesprochen besteht die Aufgabe
also darin, eine Entmischungsmatrix Wij derart zu schätzen,
daß die ursprüngliche (unbekannte) Mischungsmatrix Aij
invertiert wird.
Ein sehr effizienter iterativer Algorithmus zur Quellentrennung basiert
auf der Minimierung der paarweisen Kreuzkorrelationen der entmischten Signale.
Dabei stellt man zunächst eine Fehlerfunktion auf

Ein mathematisch sehr elegantes Verfahren beruht auf linearer Algebra. Dort wird Wij auf direktem Wege durch eine simultane approximative Diagonalisierung eines Satzes geeignet definierter Matrizen (z.B. Korrelationsmatrizen) ermittelt. Eine Besonderheit dieses Ansatzes zur Quellentrennung besteht darin, daß hier lediglich die statistischen Eigenschaften der Signale, wie Korrelationen, Kurtosis oder Transinformation, benutzt werden. Da insbesondere Korrelationen verhältnismäßig einfach und robust aus Daten geschätzt werden können, ist dies für die Anwendung auf reale Probleme sehr vorteilhaft. Beispielsweise stellte sich heraus, daß unter der Voraussetzung einer räumlich-zeitlichen Struktur in den gemessenen Daten (Mikrofonsignale) korrelationsbasierte Algorithmen sogar bessere Trennungsergebnisse liefern als Verfahren, die auf Frequenzfiltern beruhen.
In realen akustischen Umgebungen gestaltet sich die Lösung des Cocktailparty-Problem durch das Auftreten von Echos und Hall noch komplizierter. Man kann jedoch zeigen, daß sich dieses schwierigere Quellentrennungsproblem mittels Kurzzeitfouriertransformationen auf das ursprüngliche (oben besprochene) und einfacher lösbare Problem der unverzögerten Überlagerungen zurückführen läßt.
Wenn es gelingt, die vorhandenen Algorithmen weiter zu verbessern, so daß sie eine Quellentrennung auch in großen Räumen (lange Echos) und bei beweglichen Quellen gestatten, so sind zukünftig zahlreiche Anwendungsmöglichkeiten denkbar, wie digitale Hörhilfen, Geräuschunterdrückung für Spracherkennungs- oder Telekonferenzsysteme und vieles mehr.
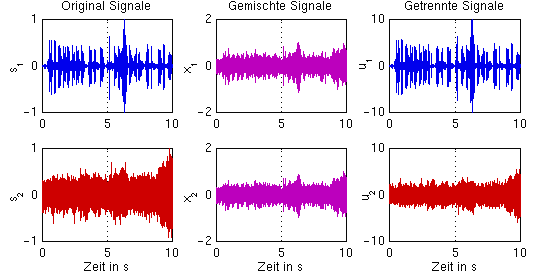
Abbildung: Zwei unabängige Signale (links) überlagern sich linear und unverzögert. Mit zwei Sensoren (Mikrofonen) werden zwei unterschiedliche Mischungen gemessen (Mitte) und daraus werden die beiden unbekannten Originalsignale rekonstruiert (rechts).
Unsere Resultate sind jedoch auch zum jetzigen Zeitpunkt schon für
praktische Anwendungen in der Medizintechnik von unmittelbarer Bedeutung,
denn bemerkenswerterweise ist ein ganz ähnliches Verfahren, wie das
ursprünglich zur Lösung des Cocktailparty-Problems in der Akustik
entwickelte, auch zur Eliminierung von Störungen (Artefakten)
in biomedizinischen Meßdaten geeignet.
So treten bei Elektro- (EEGs) oder Magnetoencephalogrammen (MEGs),
d.h. bei Messungen der elektrischen bzw. magnetischen Felder von Hirnströmen,
immer wieder Artefakte auf, die durch Muskelzuckungen, den Herzschlag oder
Augenbewegungen verursacht werden und nicht selten um einige Größenordnungen
stärker sind als das zu messende Hirnsignal. Artefakte stellen also
für die Analyse von EEGs bzw. MEGs ein erhebliches Problem dar und
behindern die medizinische Diagnose.
Während sich manche technischen Artefakte, wie Störungen durch das Stromnetz (50 Hz Netzbrummen), durch Frequenzfilter eliminieren lassen, besitzen viele nichttechnische Störungen eine ähnlich breitbandige Charakteristik wie die zu messenden Hirnsignale. Basierend auf der Annahme der statistischen Unabhängigkeit der Quellen erlauben es unsere Verfahren, ein räumliches Filter zu konstruieren, daß den artefaktfreien Teil des gesamten Zustandsraums repräsentiert und somit Störungen unterdrückt. Durch geeignete Rückprojektion in den Signalraum kann dann ein artefaktfreies EEG bzw. MEG rekonstruiert werden.
Eine solche Möglichkeit der Artefaktkorrektur unter annähernder Erhaltung aller Signale kortikaler Quellen ist ein bedeutender Fortschritt, mit dem zukünftig eine Verkürzung der Meßzeiten bei EEG- und MEG-Aufnahmen und nicht zuletzt eine Erhöhung der Diagnosesicherheit erreicht werden kann.
Literatur
Adresse
Dr. Klaus-Robert Müller
Andreas Ziehe
GMD FIRST
Kekuléstr. 7
12489 Berlin
Email: klaus@first.gmd.de
Email: ziehe@first.gmd.de
WWW: http://www.first.gmd.de/persons/Mueller.Klaus-Robert/IDA.html
Lebenslauf
Dr. Klaus-Robert Müller (34 Jahre) ist seit 1995 als Leiter der
Arbeitsgruppe für "Intelligente Datenanalyse" bei der GMD FIRST in
Berlin tätig. Die Gruppe beschäftigt sich schwerpunktmäßig
mit computergestützten Datenanalysemethoden wie Independent
Component Analysis (ICA), Support Vektor Maschinen und der Analyse nichtstationärer
Zeitreihen. Herr Müller hat von 1984 bis 1992 Physik und Informatik
an der Universität Karlsruhe studiert. Nach der Promotion in Informatik
(1992) mit einem Thema über neuronale Netzwerke war Herr Müller
bei der GMD FIRST als Postdoc tätig. 1994 folgte ein einjähriger
Gastaufenthalt an der University of Tokyo bei Prof. Amari. Herr Müller
war ferner zu Kurzaufenthalten bei AT&T Bell Labs und Microsoft. In
1999 erhielt den Ruf auf eine Professur für Neuronale Netze und Zeitreihenanalyse
an der Universität Potsdam.
Für seine Arbeiten wurde Dr. Müller mehrfach ausgezeichnet.
Zum Beispiel erhielt er mit seiner Arbeitsgruppe den Preis für das
beste Wissenschaftlich-Technische Projekt der GMD 1996 und 1998,
außerdem den Olympus Preis 1999 der Deutschen Gesellschaft für
Mustererkennung (DAGM) für seine Arbeiten auf dem Gebiet der Mustererkennung.
Andreas Ziehe (27 Jahre) hat an der Humboldt-Universität zu Berlin
Informatik studiert und ist seit seinem Informatikdiplom (1998) als Wissenschaftler
bei der GMD FIRST tätig. Seine Forschungsinteressen liegen auf dem
Gebiet der Datenanalyse und Signalverarbeitung. Schwerpunkt ist die Weiterentwicklung
und Anwendung von Methoden zur Signalquellentrennung auf neurophysiologischen
Daten (EEG und MEG).
Herr Ziehe wurde 1998 innerhalb der GMD mit dem Preis für die
beste Diplomarbeit ausgezeichnet.
Glossar
Kurtosis: Dimensionsloser Zahlenwert,
der die graphische Gestalt von statistischen Verteilungen beschreibt im
Vergleich zur Gaussverteilung. Hohe Kurtosiswerte weisen auf ein breite,
relativ flache Verteilung, niedrige Werte auf eine schmale, relativ spitze
Verteilung hin. Die Kurtosis der Gaussverteilung ist gleich Null. Für
die Quellentrennung ist die Kurtosis vom Bedeutung, da die Verteilungsfunktion
von gemischten Signalen in Richtung Gaussverteilung tendiert.
Transinformation: in der Informationstheorie eine Größe, die den Grad der Abhängigkeit zweier stochastischer Variablen voneinander beschreibt, indem sie quantifiziert, wieviel Information man über die eine Variable gewinnt, wenn man die andere kennt.
|