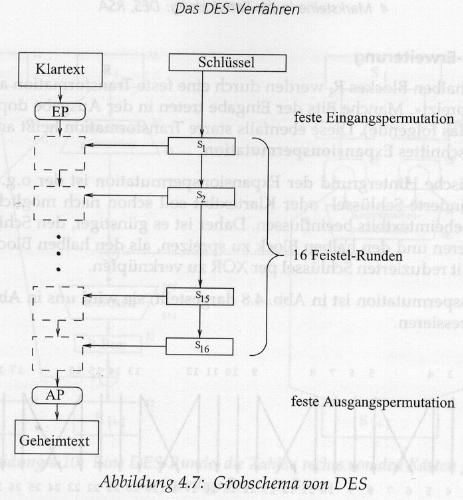
Der Algorithmus

DES ist ein Produktalgorithmus. Er

verwendet ein 56 Bit langen Schlüssel, um

blockweise 64 Bit Klartext in 64 Bit Geheimtext zu überführen bzw. umgekehrt. Das geschieht
in 16 schlüsselabhängigen Runden. Vor der ersten und nach der letzten Runde werden 
jeweils eine feste , bitweise Transposition (d.h. Permutation) durchgeführt. Dabei ist die abschließende Permutation die Umkehrung der ersteren. 

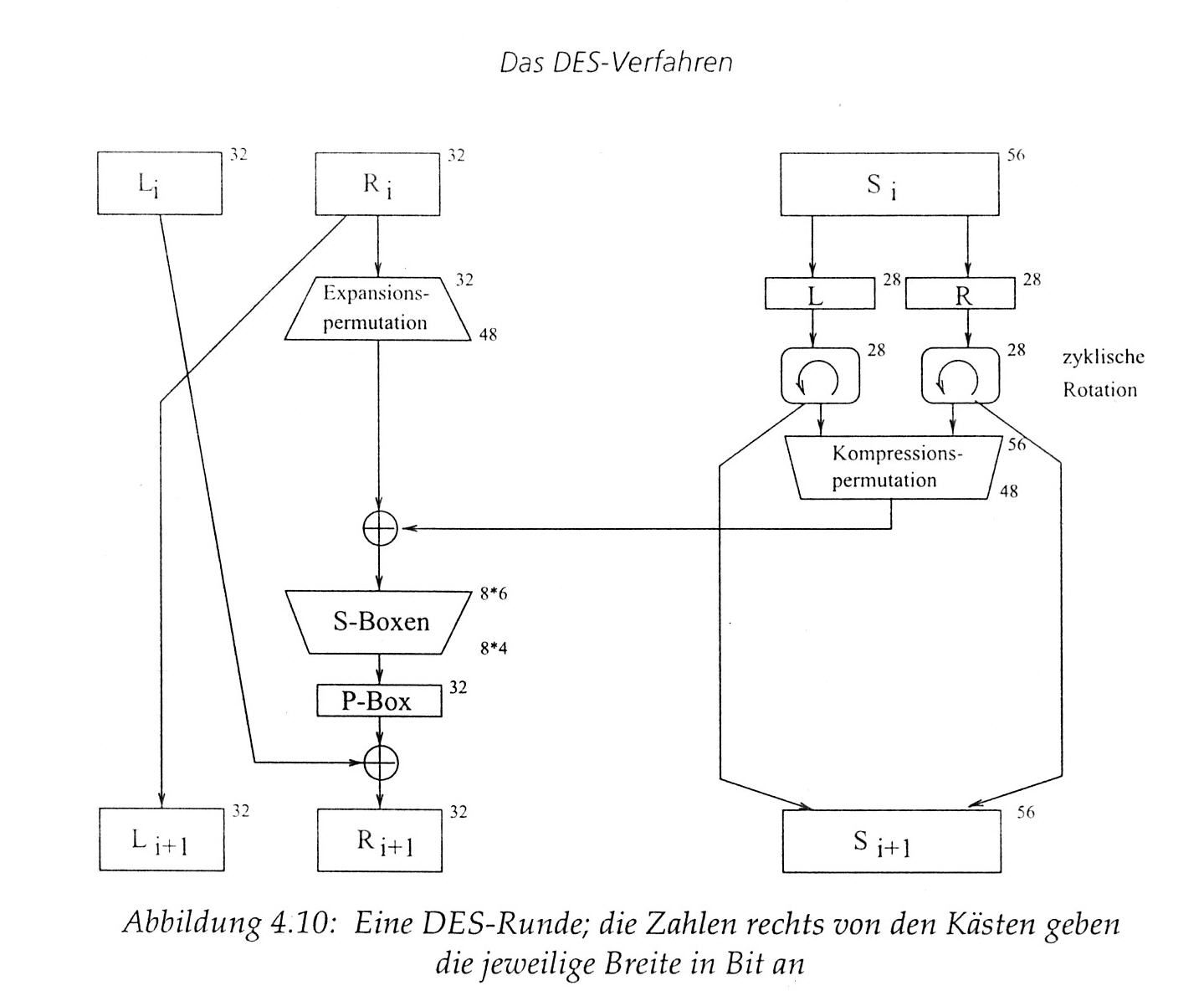
Aufbau der runden- und schlüsselabhängigen Funktion f bei DES

Zunächst wird der 56 Bit Schlüssel in Abhängigkeit von der Runde verändert, 48 Bit davon werden ausgewählt
Dann wird die rechte Blockhälfte R_i von 32 auf 48 Bit erweitert (Lawineneffekt: jedes geänderte Schlüssel- oder Klartextbit soll schon nach wenigen Runden alle Geheimtextbits beeinflussen.)
Beide 48 Bit Folgen werden nun per XOR verknüpft.
Die 48 Bit werden in 8 Gruppen zu je 6 Bits aufgeteilt.
Mittels acht S-Boxen wird das ganze in eine 32 Bit Folge transformiert .(Eine S-Box ist eine Tabelle mit 4 Zeilen und 16 Spalten; größter vorkommender Tabelleneintrag: 15) 

Die 32 Bit Folge wird permutiert, d.h. Ihre Reihenfolge geändert. Diese Transformation wird durch die P-Box beschrieben. (Die P-Box ist einfach eine bestimmte Anordnung der Zahlen von 1 bis 32)

Der entstandene 32 Bit Block wird per XOR mit der linken Blockhälfte L_i verknüpft.

Dadurch ergibt sich die rechte Blockhälfte der neuen Runde.
 
 

Sehen wir uns noch einige Details an.
 

Eingangs- und Ausgangspermutation

Die Permutationen vor der ersten und nach der letzten Runde dienen keiner Sicherheit. Vermutlich liegt ihre Verwendung in der Hardware begründet, denn Mitte der 70er Jahre war es noch nicht so einfach, 64 Bit Daten in ein Register zu laden: Es gab noch nicht einmal 16 Bit Mikroprozessoren.
 
 

Schlüsseltransformationen

Vor jeder Runde zerlegen wir den 56 Bit Schlüssel in zwei 28 Bit lange Hälften und rotieren jede Hälfte in Abhängigkeit von der Rundennummer um 1 oder 2 Bit. »Rotieren« heißt hier: Alle Bits wandern 2 Stellen nach links; die beiden Bits, die dabei links herausfallen, wandern auf den beiden rechten Plätzen wieder herein. Danach setzen wir beide Hälften wieder zu einem 56 Bit Schlüssel zusammen.

Nun wählen wir nach einem festen Schema 48 der 56 Bits aus und permutieren sie gleichzeitig, d.h., wir verändern ihre Anordnung. Weil sich die Zahl der Bits bei diesem Vorgang reduziert, nennt man ihn Kompressionspermutation.

Dank dieser (starren) Schlüsseltransformation kommen in jeder Runde andere Schlüsselbits zum Einsatz, jedes Bit in etwa 14 Runden, allerdings nicht ganz gleichmäßig verteilt. 
 
 

Die Halbblock Erweiterung

Die 32 Bit des halben Blockes R_i werden durch eine feste Transformation auf einen 48 Bit Block »gespreizt«. Manche Bits der Eingabe treten in der Ausgabe doppelt auf. Diese ebenfalls starre Transformation heißt Expansionspermutation.
 
 

Die S Boxen

Bis jetzt haben wir einen 48 Bit Block als Ergebnis der letzten XOR Operation vorliegen. Diese 48 Bits teilen wir nun in 8 Gruppen zu je 6 Bits auf und transformieren jede Gruppe mit einer anderen sogenannten S Box (der Name bedeutet substitutionbox). Diese acht S Boxen stellen den kritischsten Teil von DES dar. Jede S Box ist eine Tabelle mit 4 Zeilen und 16 Spalten und wandelt 6 Eingabebits in 4 Ausgabebits um. Diese Tabelle wenden wir wie folgt an: Wenn die Eingabe aus den sechs Bits b1,...,b6 besteht, dann legt die aus b1 und b6 bestimmte Zahl (2 Bits = 4 Werte) die Zeile der Tabelle fest, die aus den vier restlichen Bits (b2b3b4b5) bestimmte Zahl dagegen die Spalte. Die Zahl in der entsprechenden Zeile und Spalte ist der Ausgabewert.
 
 

Design des Algorithmus (Vorteile)

Der DES Algorithmus erscheint ziemlich kompliziert, ist aber extrem hardwarefreundlich. In keinem Schritt wird addiert oder gar multipliziert, alles beschränkt sich auf bitweise Verschiebungen, feste Permutationen und die XOR Operationen. Hinter dieser Komplexität steckt ein System:

Die Erweiterungspermutation und die P-Boxen sorgen für Diffusion.
Die P-Boxen sorgen dafür, daß ein Klartextbit bei jeder Runde eine andere S-Box durchläuft.
Die S-Boxen bringen Nichtlinearität und Immunität gegen differentielle Kryptanalyse hinein.
Die Rotation und Kompressionspermutation sorgen dafür, daß jede Änderung eines Schlüsselbits schon nach wenigen Runden alle Geheimtextbits beeinflussen.

Brute Force
differentielle und
lineare Kryptanalyse 

DES ist nicht sicher gegen Geheimdienste und große Konzerne.
 

Vorwort

Einführung

Geschichte

Grundbegriffe

DES

RSA

Protokolle

Signaturen

Abschlußbetrachtung

Quellen