|
Die Schätzübung auf Seite 2 macht deutlich,
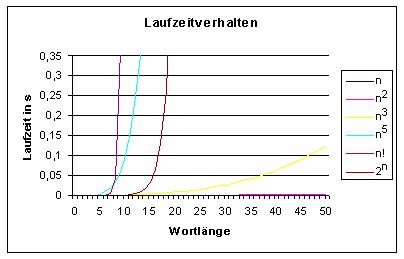
dass große polynomielle (z.B. n5), aber noch mehr die exponentiellen Funktionen (z.B. 2n) die Verarbeitungszeit schnell anwachsen lassen.
Die folgende Grafik gibt einen Überblick über das Lauzeitverhalten hypothetischer Programme mit häufigen Komplexitäten.
Wieder wird angenommen, dass der verarbeitende Prozessor 1.000.000 Operationen in der Sekunde ausführen kann.
|
- Diese Funktionen sind ohne Frage eindrucksvoll, aber wann hat ein Programm schon mal genau die Komplexität von n2?
Oft gibt es mehrere Schleifen, auch innerhalb von Schleifen und eine Reihe einfacher Operationen.
- Hier nun erfolgt eine Vereinfachung.
Man will nicht wissen, wie schnell das Programm genau ist, sondern in welche Größenordnung sein Verhalten einzuordnen ist.
Die Komplexitätsklasse, der allgemeine qualitative Verlauf, ist interessant. Unwichtig ist das konkrete Verhalten.
Dabei kann man sich auch auf folgende Aussage stützen:
 |
Eine Funktion h ist in der Klasse O(f)
gdw. es eine (positive) Konstante c gibt,
so dass für alle Werte n größer als ein dazu gewählter Startwert n0
jeder Funktionswert von h kleiner (oder gleich groß) bleibt als das Produkt aus Konstante und Funktionswert von f.
(allein die Beträge werden betrachtet)
|
Umgangssprachlich könnte man formulieren, dass f ungefähr das gleiche Wachstumsverhalten wie h aufweist.
Typische Klassen wären n, n2, n3, n5, 2n oder nn.
Beispiel:
Sei h(n)=2n2-6n+5 und
f sei n2.
h liegt in der Klasse O(f). Dabei ist c=2 und n0=1.
h(n) ist immer kleiner als 2 * f(n).
|
|
Benutzer: Gast •
Besitzer: matthias • Zuletzt geändert am:
|
|
|
1
2
3
4
5
Beispiel