|
Eingabe: eine kontextfreie Grammatik G = (N,T, P, S) ohne Linksrekursion und ein Eingabewort w = x1x2 · · · xn mit
n > -1.
Die Produktionen in P sind nummeriert 1, 2, . . . , p.
Ausgabe: Linksparse, wenn existent, sonst "Fehler"
Methode:
- Für jedes A aus N ordne die Alternativen (alternates). Ai ist der der Index für die i-te Alternative von A.
- Eine Konfiguration wird durch das 4-Tuple (s, i, L1, L2) beschrieben; mit
- s: Zustand des Algorithmus. Der Algorithmus kann sich in den Zuständen q (normaler Modus), b (Backtracking) oder t (Terminiert) befinden.
- i: Index des Inputzeigers, dabei wird angenommen, dass an der Stelle n + 1
auf die Endmarkierung $ gezeigt wird.
- L1 ist die erste push-down-Liste, sie speichert Informationen zum bisherigen Ableitungsverlauf.
Dazu enthält sie die Nummern der verwendeten Regeln - kodiert durch das expandierte Nichtterminalsymbol Ai und der Nummer der Alternative einerseits,
andererseits die bereits erkannten Inputsymbole.
- L2 ist die zweite push-down-Liste (L2) aus (N
 T)*.
Diese Liste enthält die aktuelle Linkssatzform der Analyse, sie verhält sich wie ein Keller. T)*.
Diese Liste enthält die aktuelle Linkssatzform der Analyse, sie verhält sich wie ein Keller.
Ein Lesekopf erkennt jeweils das letzte Symbol von L1, bzw. das erste Symbol von L2.
- Die Ausgangskonfiguration ist (q, 1,
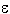 , S$). , S$).
- Es gibt sechs verschiedene Schrittmöglichkeiten, die durch Konfigurationsübergänge von
(s, i, L1, L2) nach (s', i', L1', L2') charakterisiert werden können:
- Expansion: (n, i, L1, AL2) |- (n, i, L1A[1],
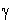 L2),
falls A L2),
falls A  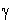 die erste Alternative von A ist. die erste Alternative von A ist.
- Erfolgreicher Abgleich von Eingabe- und abgeleiteten Symbol: (n, i, L1, a) |- (n, i + 1, L1a, RestL2)
- Erfolgreiche Terminierung: (q, n+1,
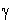 , $) |-
(t, n+1, , $) |-
(t, n+1,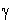 , ,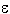 ).
Homomorphismus zur Ausgabe des Linksparse: h(a) = a für alle a aus T; h(A[i]) = p, wobei p die Regelnummer der i-ten Alternative von A ist. ).
Homomorphismus zur Ausgabe des Linksparse: h(a) = a für alle a aus T; h(A[i]) = p, wobei p die Regelnummer der i-ten Alternative von A ist.
- Keine Übereinstimmung von Eingabe- und abgeleiteten Symbol: (q, i, L1, aL2) |- (b, i, L1, aL2),
falls xi
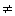 a a
- Backtracking: (b, i, L1a, L2) |- (b, i - 1, L1, aL2) für alle a aus T.
- Probieren der nächsten Alternative: (b, i, L1A[j] ,
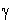 jL2) |- jL2) |-
- (q, i, A[j+1],
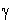 j+1L2), wenn j+1L2), wenn 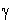 j+1 die Alternative j + 1 von A ist. j+1 die Alternative j + 1 von A ist.
- Keine neue Konfiguration, wenn i = 1 und A = S und S nur j Alternativen hat.
(An dieser Stelle sind alle Alternativen, das Wort abzuleiten, erschöpft).
- (b, i, L1, AL2) sonst. (Die Alternativen für A sind erschöpft, mit dem Backtracking wird fortgefahren
nachdem das Ersetzen von A[j] durch seine rechte Regelseite rückgängig gemacht wurde.)
Ablauf des Algorithmus:
1. Schritt: Berechne fortlaufend Konfigurationen bis keine weitere Konfiguration berechnet werden kann.
2. Schritt: Hat die zuletzt berechnete Konfiguration die Form (t, n+1, 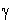 , , 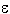 ), dann halte und gib h( ), dann halte und gib h(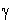 ),
den ersten Linksparse, aus. Sonst signalisiere "Fehler". ),
den ersten Linksparse, aus. Sonst signalisiere "Fehler".
|
 1
2
3
4
5
1
2
3
4
5
 Üben
Üben