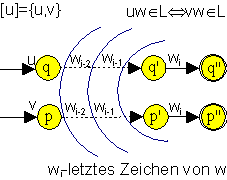
Bei der Suche nach verschmelzbaren Zuständen
werden Eigenschaften von Äquivalenzklassen berücksichtigt. Die
Teilwörter u und v sind in den Zuständen p und q abgearbeitet.
Wird nun jeweils ein Teilwort w angehangen und es entstehen in beiden Fällen
Wörter, die nicht in der Sprache liegen, oder in beiden Fällen
Wörter, die in der Sprache liegen, dann ist nicht wichtig, ob das
Wort in unterschiedlichen Endzuständen akzeptiert wurde.
Diese Eigenschaft nutzt der Algorithmus. Von
Endzuständen ausgehend arbeitet er sich bis zum Startzustand vor.
Dabei wird überprüft, ob von den verglichenen Zustandspaaren
aus unterschiedliche Analysen eines Wortes möglich sind. |
|
Für jeden DEA M gibt es einen M' mit minimal vielen Zuständen,
der die gleiche Sprache akzeptiert, also L(M)=L(M').
Das Verfahren sucht nach Äquivalenzklassen. Es wird ausgenutzt,
dass sich äquivalente Teilwörter in Bezug auf Konkatenation funktional
gleich verhalten.
Algorithmus zum Auffinden der verschmelzbaren Zustände (indistinguishable
states)
E: DEA M = (Q,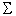 , ,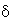q0,F})
ohne überflüssige Zustände (s. Reduktion).1
A: Verschmelzbare Zustände (ohne Markierung)
-
Bilde Tabelle mit Zustandspaaren {q,q'} und 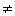q
 q'
Eine halbe Matrix reicht hier aus, da die Reihenfolge
im Paar keine Rolle spielt, {q,q'} = {q',q}.
-
Markiere alle Paare {q,q'}, bei denen einer(!) Endzustand ist und der andere
nicht.
In dem Fall sind q und q' auf keinen Fall äquivalent.
Dies ist unsere Initialisierung.
-
Für jedes unmarkierte Paar und jedes a aus
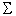tue folgendes:
markiere das Paar, wenn das Paar {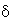(q,a), 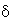(q',a)}
bereits markiert ist;
bis keine weitere Änderung mehr eintritt.
Vorgehen von "hinten": q und q' sind dann äquivalent,
wenn sie in ein verschmelzbares Zustandspaar = in einen Zustand hineinführen
-
Die noch unmarkierten Zustandspaare sind jeweils verschmelzbar.
Das Verfahren kann mit der Komplexität O(|Q|2) implementiert
werden.
____
1 Bitte beachten Sie, dass Automaten immer vollständig definiert sind (Konzept: absorbierender Zustand).
Insofern sind Graphdarstellungen oft vereinfacht.
|
1
2
3
4
5
6
Beispiel