Suche Home Einstellungen Anmelden Hilfe

2.3.3 Greibach-Normalform (GNF):

Ziel: Jede Regel hat die Form A - > a W mit A aus N, a aus T und W aus N* (-Regeln ausgenommen) Start: kontextfreie Grammatik ohne Linksrekursion und Kettenregeln
Bei der folgenden Regeltransformation bleibt die generierte Sprache gleich. Alle Vorkommen eines Nichtterminals 'B' werden jeweils durch die rechte Seite aller "B-Regeln" ersetzt. "B-Regeln" sind Regeln, in denen das Nichtterminal 'B' expandiert wird, also 'B' auf der linken Regelseite steht.	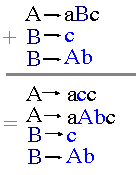Eine A-Regel ist eine Regel mit dem Nichtterminal A auf der linken Seite. Gegeben sei eine Grammatik G mit einer A-Regel A-> w1 B w2. B-> b1 | b2 | ... | bn ist die Menge aller B-Regeln (w1, w2, b1 ... bn aus (N U T)*. Für eine neue Grammatik G1 entfernt man aus P die Regel A-> w1 B w2 und fügt statt dessen A -> w1 b1 w2 | w1 b2 w2 | ... | w1 bn w2 ein. Es gilt L(G) = L(G1). Gegeben eine G mit allen linksrekursiven A-Regeln A -> A w1 | ... | Awn und allen nicht-linksrekursiven A-Regeln A -> b1 | ... | bm. G1 ist eine Grammatik ohne Linksrekursion wobei alle A-Regeln durch folgende Regeln ersetzt werden. A -> bi | bi B (1<=i<=m) B -> ai | ai B (1<=i<=n) B ist ein neues Nichtterminal. (Linksrekursion zu Rechtsrekursion)	A-Regeln Regeltransformation ohne Sprachänderung       Beseitigung von Linksrekursion   Ordnung von A-Regeln

Warum darf die Grammatik keine Kettenregeln enthalten?

Greibach-Normalform 1   2   3   4   5 Schleifenlemma

Benutzer: Gast • Besitzer: matthias • Zuletzt geändert am: