| Vom 7-Tupel zum 4-Tupel
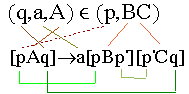 Zusammenhang zwischen Übergang und Regel
Zusammenhang zwischen Übergang und Regel
|
Konstruktion einer Grammatik auf der Grundlage eines KA
| Kellerautomat M | Grammatik G |
|---|
| Q | {S} {[pZq] | für alle p und q aus Q und jedes Z aus {[pZq] | für alle p und q aus Q und jedes Z aus  } } | |
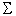 | 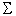 =T =T | |
 | |  wird zusammen mit den Zuständen in N kodiert wird zusammen mit den Zuständen in N kodiert |
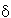 | P |
- Startregeln: S -> [q0Zp] für jedes p aus Q
- Für jeden Übergang (p,B1B2...Bk)
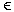 (q,a,A): (q,a,A):
[qApk] -> a [pB1p1][p1B2p2]...[pk-1Bkpk]
(für jedes beliebige p1 ... pk aus Q und ein k >=0)
|
| q0 | S | |
| # | | |
| Ø | | |
Alle Nichtterminale, nach dem Muster [Zustand1 Kellersymbol Zustand2] zusammengesetzten Symbole,
sind folgendermaßen zu verstehen:
- Zustand1 - Zustand vor Verarbeitung von Kellersymbol
- Zustand2 - Zustand nach Verarbeitung von Kellersymbol, also wenn das Symbol aus dem Keller entfernt wurde
Da der Zustand des Automaten nach der Verarbeitung eines Symbols nicht bekannt ist, werden Regeln für jeden Zustand zu P hinzugefügt.
Wieso gilt nun: [pAq] =>m w gdw. (q,w,Z) |-m (p,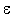 , ,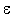 )? )?
Beweis durch Induktion:
- m=0: Für m=0 gilt weder [pAq] =>0 w noch (q,w,Z) |-0 (p,
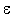 , ,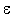 ).
Somit ist die Äquivalenz erfüllt (in einer Implikation ist die Folgerung aus etwas Falschem immer wahr) ).
Somit ist die Äquivalenz erfüllt (in einer Implikation ist die Folgerung aus etwas Falschem immer wahr)
- Induktionschritt: [pAq] =>m+1 w existiert gdw. (q,w,Z) |-m+1 (p,
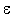 , ,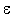 ). ).
- "=>"
- "<="
|
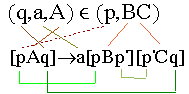
 1
2
1
2
 Kontextfreie Grammatiken und Kellerautomaten
Kontextfreie Grammatiken und Kellerautomaten