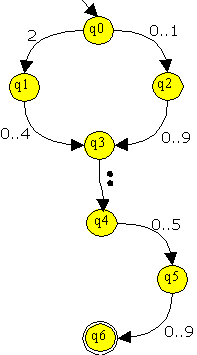
Pfeile, die z.B. mit 0 .. 9 beschriftet sind, stehen als Abkürzung für eine ganze
Reihe von Pfeilen, die jeweils mit 0, 1, 2 usw. beschriftet sind.
|
Ein endlicher Automat lässt sich mit einem gerichteten Graphen assozieren.
Dabei bilden die Zustände die Knoten und die Transitionen die Kanten von einem Knoten zu einem anderen.
Die Knoten werden als Kreise dargestellt, die Kanten als Pfeile. Endzustände werden durch einen Doppelkreis gekennzeichnet.
Der Startzustand wird durch einen zusätzlichen hereingehenden Pfeil gekennzeichnet.
Jede Kante ist mit einem Label versehen, das dasjenige Symbol enthält,
das beim Übergang zwischen den zwei beteiligten Zuständen verarbeitet wird.
Kanten, von und in den gleichen Zustand - sogenannte loops - entstehen, wenn ein Eingabezeichen ohne einen Zustandswechsel
verarbeitet wird.
Besondere Übergänge sind die "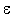 -moves"
( -moves"
(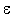 -Übergänge).
Dabei erfolgt ein Übergang in den Folgezustand unabhängig von der Eingabe.
Der Lesekopf wird bei einem " -Übergänge).
Dabei erfolgt ein Übergang in den Folgezustand unabhängig von der Eingabe.
Der Lesekopf wird bei einem "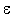 -move" nicht weiter bewegt. -move" nicht weiter bewegt.
Welche Wörter erkennt der Automat im Beispiel?
Wie viele Möglichkeiten hat der Automat, wenn er im Zustand q0 das Zeichen '0' liest?
Ist seine Arbeitsweise deterministisch oder nicht-deterministisch, d.h. treten bezüglich eines Eingabezeichens
Konflikte über den Folgezustand auf?
|

 1
2
3
4
5
1
2
3
4
5
 Deterministische Endliche Automaten
Deterministische Endliche Automaten