Reguläre Grammatiken
Reguläre Ausdrücke
Reguläre Sprachen
|
A -> a A = A -> a1 a2 ... an A
Wie sicher schon durch den Namen reguläre Sprachen angedeutet besitzt man mit regulären Ausdrücken
und regulären Grammatiken ein äquivalentes Beschreibungsmittel zur Darstellung der regulären Sprachen.
Basis: G= ({S},T,P,S)
| RA | mit P | L(G) |
|---|
| Ø | Ø | Ø |
| e | {S -> e} | {e} |
| a (für alle a in T) | {S -> a} | {a} |
Sind L1 und L2 rechtslineare Sprachen, dann sind auch
| RA | G | mit P |
|---|
L1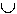 L2 L2 |
(N1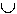 N2 N2 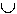 {Sneu}, T,P,Sneu) {Sneu}, T,P,Sneu) |
P1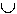 P2 P2 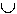 {Sneu -> S1 | S2} {Sneu -> S1 | S2} |
| L1L2 |
(N1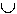 N2}, T,P,S1) N2}, T,P,S1) |
P1'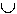 P2 P2
P1' ist wie P1, aber jede Regel der Form A -> a wird modifiziert zu A -> aS2. |
| L1* |
(N1,T,P,S1) |
wie P1, aber zu jeder Regel der Form A -> a wird zusätzlich eine Regel A -> aS1 eingefügt. |
|
 Schleifenlemma
Schleifenlemma