|
Ein Verfahren, um zu zeigen, dass Sprachen nicht regulär sind, ist das Pumping- oder
Schleifenlemma. Nach Jurafsky & Martin (2002) liegen dem Pumping-Lemma zwei Annahmen zugrunde.
Die erste ist, dass reguläre Sprachen wie anbn nicht von einem
endlichen Automaten verarbeitet werden können, da dieser nur über eine endliche Anzahl von
Zuständen verfügt. Die zweite Annahme besagt, dass wenn die Wörter einer reguläre Sprache größer als die Anzahl
von Zustände sind, dann muss es der Automat irgendwo eine Schleife haben. Das heißt also, dass
eine Sprache, die diese Schleife nicht aufweist, nicht regulär ist.
Vereinfacht gesagt, bedeutet also die Anwendung des Schleifenlemmas, dass man in einer
(nicht-regulären) Sprache ein Zeichen findet, an das man "aufpumpen" kann.
Da die Sprache nichtregulär ist, findet man dieses Zeichen nicht, und man kann
daher davon ausgehen, dass die Sprache nicht regulär ist.
Formale Definition des Pumpinglemmas
Sei L eine reguläre Sprache. Dann gibt es eine Zahl n > 0, so dass sich
jedes Wort x 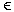 L mit |x| <= n als x=abc schreiben lässt und abic L mit |x| <= n als x=abc schreiben lässt und abic 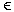 L für alle i <= 0. L für alle i <= 0.
Ein Beispiel
Nehmen wir an, L sei das Wort einer Sprache und M sei ein endlicher Automat mit n Zuständen.
Der Automat startet im Zustand q0, und geht nach dem Lesen des ersten Symbols in den
Zustand q1. Nach dem Lesen von n Symbolen wird der Automat im Zustand qn sein. Dies
bedeutet, das der Automat n+1 Zustände durchlaufen hat (q0 bis qn). Da der Automat
jedoch nur n Zustände hat, müssen zwei Zustände, z.B. qi und qj die selben sein.
Dies bedeutet, dass in einem der Zustände eine Schleife sein muss.
In dem unten dargestellten Beispiel wird dieser Aspekt illustriert. Der Automat hat 3 Zustände (n =3) und das Wort der
Sprache 3 Zeichen. Um jedoch das Wort ohne eine Schleife verarbeiten zu können müsste der Automat 4 Zustände (n+1)
haben. Da dies nicht der Fall ist, ist die Sprache abic nicht regulär ist.
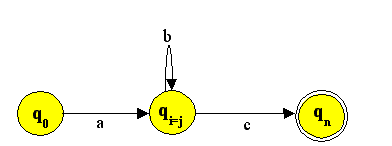 Abb. Darstellung des Pumping-Lemmas. Adaptiert nach Jurafsky & Martin (2000, S.483).
Abb. Darstellung des Pumping-Lemmas. Adaptiert nach Jurafsky & Martin (2000, S.483).
|

 1
2
1
2
 Übersicht: Sprachklassen
Übersicht: Sprachklassen