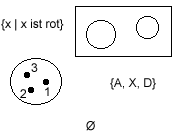
Mengennotation: wie bereits gesehen in geschweiften
Klammern {}, wobei man alle Elemente aufzählt. Diese Darstellungsvariante
wird auch für unendliche Mengen genutzt, z. B. {2, 3, 5, 7, 11, ... }. Allerdings können die Auslassungspunkte zu Mehrdeutigkeiten
führen.
|
Da wir Sprachen als Mengen begreifen, ist es nützlich, die Operationen
auf Mengen zu kennen.
Mengen enthalten Objekte aus einem vorgegebenen Bereich, dem Universum
- einer Art Obermenge. Das Universum bilden z. B. die natürlichen Zahlen, die
lateinischen Buchstaben, alle Objekte in einem Büro . . . Dabei wird keine
Reihenfolge der Objekte bestimmt und jedes Element kann nur einmal vorkommen.
Nehme ich also bspw. die Menge {roter-Socken, schwarzer-Stiefel, güner-Mantel},
so ändert sich an dieser Menge nichts, wenn ich grüner-Mantel hinzufüge.
Füge ich hingegen das Objekt schwarzer-Halbschuh hinzu, so erhalte ich die Menge
{roter-Socken, schwarzer-Stiefel, schwarzer-Halbschuh, güner-Mantel}. Die Objekte
bezeichnet man auch als Elemente einer Menge.
Es ist auch möglich, die Elemente durch eine Eigenschaft E zu
kennzeichnen: M = { x | x hat E } . Graphisch werden Mengen durch geschlossene Figuren
(Kreis, Rechteck o. ä. bei zwei Dimensionen) repräsentiert. Eine besondere
Menge ist die leere Menge: M = Ø.
|
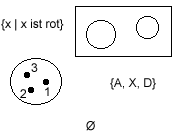
 Operationen auf Mengen
Operationen auf Mengen