|
| |||||||||||
|
Bei den Transpositionschiffren bleiben die zu verschlüsselnden "Buchstaben, was sie sind, sie bleiben aber nicht wo sie sind" Es wird also lediglich die Reihenfolge der Buchstaben verändert. Eine Transpositionschiffre erhält man beispielsweise, indem man einen Text spaltenweise statt zeilenweise aufschreibt, dann aber zeilenweise übermittelt. Dem Empfänger müssen dann, quasi als Schlüssel, die Anzahl der Zeilen bekannt sein.
Beispiel: Aus "Dieser Text ist geheim" wird durch Umwandlung
mittels des beschriebenen Verfahrens und einer Zeilenanzahl von 5
D R I H I T S E E E T I S X G M E T E Xdie auf den ersten Blick unlesbare Botschaft "DRIHITSEEETISYGMETEX"
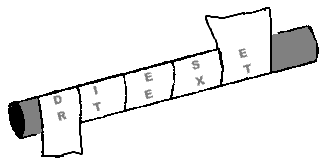
Diese Art der Codierung wurde bereits in der Antike von den Griechen benutzt. Zum Übermitteln von Geheimbotschaften verwendete man eine sogenannte "Skytale", ein Holzstab mit einem festgelegten Durchmesser, um denn dann spiralförmig Pergamentstreifen gewickelt wurde, den der Sender dann von links nach rechts beschrieb.
Die im Bild gezeigte Skytale würde dem oben beschriebenen Zeilen-/Spaltenverfahren entsprechen. Würde man den Pergamentstreifen von oben nach unten lesen, erhielte man nur "ETEXSXGMITSEDRIH", erst, wenn er um eine Skytale mit gleichem Durchmesser gewickelt würde, könnte man den Text wieder lesen.
Dieses Verschlüsselungsverfahren ist allerdings nicht sehr sicher, da es durch simples Ausprobieren in relativ kurzer Zeit geknackt werden kann. Trotzdem spielen Transpositionschiffren auch in modernen Algorithmen eine Rolle, wo sie beispielsweise zum nochmaligen Verschlüsseln bereits mit anderen Methoden verschlüsselter Texte eingesetzt wird.
Das Gegenstück zu den Transpositionschiffren bilden die Substitutionschiffren, die im folgenden vorgestellt werden.
Auch monoalphabetische Substitutionen wurden bereits in der Antike eingesetzt.
Ein Beispiel für eine monoalphabetische Substitution ist beispielsweise
der sogenannte "Caesar-Code", der auf Julius Caesar zurückgeht. Das
Geheimalphabet erhält man, indem man das Klartextalphabet um eine
bestimmte Buchstabenanzahl verschiebt, also beispielsweise:
| Klartext: | A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
| Geheimtext: | D E F G H I J K L M N O P Q R S T U V W X Y Z A B C |
Der Schlüssel ist in diesem Falle der Anfangsbuchstabe des Geheimalphabets, also hier D.
Eine andere, ebenfalls schon sehr alte Form der monoalphabetischen Substitution ist das "Atbash". Bei diesem Verfahren wird das normale Alphabet einfach umgekehrt, d.h. aus A wird Z, aus B wird Y usw. Das Atbash-Verfahren ähnelt dem römischen Caesar-Code, ist aber jüdischen Ursprungs.
Es sind jedoch auch gänzlich andere monoalphabetische Zuordnungen denkbar. Man könnte ja einem Klartextbuchstaben jeden beliebigen anderen Buchstaben oder auch eine Ziffer oder ein geheimes Symbol zuordnen, solange dies eindeutig geschieht. Alle monoalphabetischen Substitutionen haben gemeinsam, daß sie auf äußerst einfach Art realisiert werden können.
Monoalphabetische Substitutionen sind jedoch mit statistischen Verfahren ebenso einfach zu knacken, da jede Sprache eine charakteristische Buchstabenverteilung besitzt. Im Deutschen und im Englischen ist beispielsweise E der am häufigsten vorkommende Buchstabe, also wird im Geheimtext das am häufigsten vorkommende Symbol möglicherweise das E repräsentieren.
| Klartext: | DIESERTEXTWURDEGEGENUNBEFUGTESLESENGESICHERT |
| Schlüsselbuchst.: | GESICHRTGESICHRTGESICHRTGESICHRTGESICHRTGESI |
Es ergibt sich also, abhängig von der Position des Klartextbuchstaben, eine jeweils andere Cäsar-Verschlüsselung. Auch entspricht die statistische Buchstabenverteilung des verschlüsselten Textes keiner Charakteristik mehr, so daß die Zuordnung der Geheimsymbole zu den Klartextsymbolen nicht so einfach wie bei der monoalphabetischen Substitution möglich ist.
Ist jedoch die Schlüssellänge bekannt, läßt sich die Vigenère-Verschlüsselung bei der Analyse eines Geheimtextes auf Cäsar-Verschlüsselungen zurückführen, da der Schlüssel ja periodisch wiederholt wird. Betrachtet man also jedes Zeichen, das mit dem gleichen Schlüsselbuchstaben verschlüsselt wurde (in unserem Beispiel also jedes 8. Zeichen), so gehorchen diese Geheimzeichen wieder der gleichen Häufigkeitsverteilung wie bei der monoalphabetischen Substitution. Die Schlüssellänge läßt sich mit geeigneten statistischen Verfahren leicht bestimmen.
Obwohl diese Unsicherheit des Vigenère-Algorithmus natürlich bekannt ist, wird er sogar in moderner Software noch eingesetzt, zum Beispiel bei der Textverarbeitung WordPerfect.
Dies zeigt, wie wenig man sich auf diese Art von Verschlüsselung verlassen kann. Zum Glück gibt es für wichtige Daten natürlich auch Alternativen, wie die modernen Algorithmen zeigen, aber dazu später.
Da ein solcher Schlüssel natürlich nicht leicht übermittelt werden kann, ist dies auch das größte Problem dieses Verfahrens. Man könnte natürlich auf die Idee kommen, ein literarisches Werk als Schlüssel zu verwenden, die nötige Information zum Rekonstruieren der Nachricht könnte dem Empfänger leicht übermittelt werden, er braucht sich dann nur das entsprechende Werk zu besorgen. Allerdings ist die Folge von Schlüsselbuchstaben dann natürlich nicht mehr zufällig, sondern gehorcht den selben statistischen Verteilungen, die wir uns schon beim Knacken der monoalphabetischen Substitution zunutze gemacht haben. Also ist in diesem Fall keine Sicherheit mehr gewährleistet.
Abwandlungen des One-Time-Pad-Verfahrens werden manchmal auch in modernen Verschlüsselungsprogrammen verwendet. Zur Schlüsselgenerierung wird dann eine Pseudo-Zufallszahlenfolge verwendet. Die Qualität des Verfahrens hängt dann im wesentlichen von der Qualität der generierten Zahlenfolge ab.
Daher sollen im folgenden einige moderne Verfahren kurz genannt werden. Die Beschreibung kann jedoch nicht so ausführlich wie bei den einfachen Verfahren sein, da die modernen Algorithmen meist sehr viel komplexer sind und einige Mathematik voraussetzen.
Bei den Feistel-Netzwerken wird zunächst der Klartextblock in zwei gleichgroße Halbblöcke geteilt und in zwei neue Halbblöcke überführt. Als neuer linker Block wird der alte rechte Halbblock genommen, zur Berechnung des neuen rechten Halbblocks wird der alte rechte Halbblock mit einer Funktion f, die sich aus dem Schlüssel und einem veränderlichen Rundenschlüssel ergibt, verschlüsselt und anschließend mit den alten linken Halbblock bitweise Exklusiv-Oder verknüpft. Dies wird nun mehrmals, jeweils von den neuen, sich ergebenden Halbblöcken ausgehend, mit verschiedenen Rundenschlüsseln wiederholt. Ein solcher Durchlauf heißt auch eine Runde.
Die Besonderheit dieses Verfahrens besteht darin, daß man mittels Umformungen der sich daraus ergebenden Gleichungen die Geheimtexte dechiffrieren kann, ohne daß die Funktion f umkehrbar sein muß.
Wie schon erwähnt, ist der DES-Algorithmus ein solches Feistel-Netzwerk und "verwendet einen 56 Bit langen Schlüssel, um blockweise 64 Bit Klartext in 64 Bit Geheimtext zu überführen bzw. umgekehrt. Das geschieht in 16 schlüsselabhängigen Runden."
Anwendungsgebiete von DES sind neben dem Bankwesen z.B. auch die Paßwortverschlüsselung bei Unix-Systemen. Zwar gilt der DES-Algorithmus immer noch als sehr sicher, jedoch sind bestimmte Angriffe, die meistens auf ein systematisches Durchprobieren aller möglicher 256 Schlüssel hinauslaufen, nicht ausgeschlossen. Diese Angriffe haben alle gemeinsam, daß sie nur mit sehr großem Aufwand an Hardware und Zeit realisiert werden können. Eine mit DES verschlüsselte Chiffre könnte daher möglicherweise, wenn man berücksichtigt, daß das Brechen des Codes auch als Dienstleistung angeboten werden könnte, schon unter Aufwand einer "fünf- oder sechsstellige[n] Summe" geknackt werden.
Eine Lösung dieses Problems bieten jedoch die neuen, asymmetrischen Verfahren. Hierbei findet sowohl ein geheimer als auch ein öffentlicher Schlüssel Verwendung. Der geheime Schlüssel kann aus dem öffentlichen Schlüssel nicht hergeleitet werden. Da hierbei die Problematik des Schlüsselaustauschs wegfällt, wird diese Art der Chiffrierung heute sehr oft für E-Mails angewandt.
Will eine Person A einer Person B eine verschlüsselte Nachricht zukommen lassen, so benötigt A zunächst den öffentlichen Schlüssel von B. Dieser kann von B gefahrlos bekanntgegeben werden, da er nur zum Verschlüsseln dient, nicht aber zum Entschlüsseln. Hierfür benutzt B den geheimen Schlüssel, der von B unter Verschluß gehalten wird.
Einige asymmetrische Verfahren, darunter das bekannte RSA, ermöglichen darüber hinaus die Erstellung von sogenannten digitalen Unterschriften. Hierbei wird das Verfahren einfach "umgekehrt" angewandt: Der geheime Schlüssel wird zum Chiffrieren verwendet, und die erhaltene Nachricht kann dann mit dem öffentlichen Schlüssel dechiffriert werden. Damit gilt also jede Nachricht, die mit einem öffentlichen Schlüssel dechiffriert werden kann, als authentisch, da sie mit dem geheimen Schlüssel, der unter Verschluß ist, verschlüsselt worden sein muß.
Obwohl das Verfahren zu komplex ist, als daß man es hier in Kürze
beschreiben könnte, soll wenigstens der Ansatz des wohl populärsten
asymmetrischen Algorithmus, des RSA-Algorithmus, der unter anderem in dem
bekannten Programm PGP verwendet wird, kurz gezeigt werden: Möglich
wird ein solches Verfahren durch die mathematischen Probleme des diskreten
Logarithmus, also die nach x aufgelöste
Form einer Gleichung der Form
Nachteile des RSA-Verfahrens sind der hohe Zeitaufwand für das Chiffrieren und Dechiffrieren sowie die leichte Angreifbarkeit, wenn Teile des Klartextes bekannt sind. Daher wird es in gängiger Software wie z.B. PGP nur verwendet, um einen zufällig generierten und nur für eine Übermittlung benutzten "Sitzungsschlüssel" für ein symmetrisches Verfahren zu chiffrieren, mit dem der eigentliche Klartext chiffriert wird. Da der Sitzungsschlüssel selbst mit einem sicheren Verfahren verschlüsselt ist, kann er dann gefahrlos zusammen mit der mit dem symmetrischen Verfahren chiffrierten Botschaft übermittelt werden.
Die Verwendung von asymmetrischen Verschlüsselungsalgorithmen erleichtert zwar den Schlüsselaustausch, da ein Teil des Schlüssel ja öffentlich ist und nicht geheimgehalten zu werden braucht, da diese Algorithmen jedoch gerade bei E-Mail-Kontakten angewandt werden, bei der sich die Kommunikationspartner unter Umständen noch nie persönlich begegnet sind, ergibt sich die Fragestellung, ob derjenige, von dem wir den öffentlichen Schlüssel erhalten haben, auch derjenige ist, der er zu sein vorgibt. Ein potentieller Angreifer könnte beispielsweise den E-Mail-Verkehr zwischen zwei Benutzern abfangen, und beiden gefälschte öffentliche Schlüssel zuspielen, indem er vorgibt, der jeweils andere Kommunikationspartner zu sein. Jedoch läßt sich auch diese Gefahr durch geeignete Verfahren minimieren, worauf allerdings nicht näher eingegangen werden soll.
|