|
Aufbau der Dreiecksmatrix für ein Wort der Länge 5.
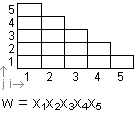 Welche Zellen und in welcher Reihenfolge werden die Zellen betrachtet?
Welche Zellen und in welcher Reihenfolge werden die Zellen betrachtet?
Die aktuelle Zelle (blau umrandet) würde jedes A enthalten, so dass A  BC in P ist und B und C im betrachteten Zellpaar liegen. BC in P ist und B und C im betrachteten Zellpaar liegen.
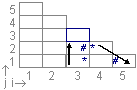
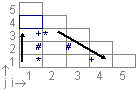 Die für die Zellen T33 (oben) und T14 (unten) überprüften Zellpaare.
Die für die Zellen T33 (oben) und T14 (unten) überprüften Zellpaare.
|
Alle Ergebnisse des Verfahrens werden in einer Dreiecksmatrix gespeichert.
Die Größe richtet sich nach der Wortlänge n.
Sei die horizontale Einteilung von 1 bis n und die vertikale Einteilung von 1 bis n.
Die Zelle T11 befindet sich unten links.
Nur Zellen "auf und unterhalb der Diagonalen" werden betrachtet.
Das sind diejenigen Zellen Tij mit
1 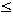 i i 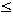 n;
1 n;
1 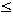 j j 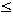 n + 1 - j. n + 1 - j.
Die Zellen werden zeilenweise von unten nach oben gefüllt.
Die Zellen einer Zeile werden von links nach rechts durchgegangen.
Für die Analyse wird das Regelformat von Grammtiken in CNF ausgenutzt.
Als erstes werden in jede Zelle der ersten Zeile alle Nichtterminale geschrieben, die das Terminal an dieser Stelle der Eingabe ableiten.
(Regeln der Form 'Nichtterminal' geht über in 'Terminal').
Anschließend werden jeweils zwei Zellen darauf hin überprüft, ob eine Kombination dort enthaltener Nichtterminale eine rechte Regelseite bildet.
Das Nichtterminal der linken Regelseite wird der aktuellen Zelle hinzugefügt. (Regeltyp: Ein Nichtterminal leitet genau zwei Nichtterminale ab.
Sei Tij die aktuelle Zelle.
Die Zellpaare ergeben sich nach folgendem Prinzip:
Alle Zellen der Spalte i von der ersten bis zur Zeile j-1 bilden die erste Komponente.
Die Zellen die in der Diagonalen nach unten rechts liegen bilden die zweite Komponente, also zunächst T(i+1)(j-1), dann T(i+2)(j-2) usw.
|
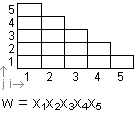
 BC in P ist und B und C im betrachteten Zellpaar liegen.
BC in P ist und B und C im betrachteten Zellpaar liegen.

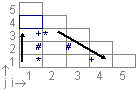
 1
2
3
4
5
1
2
3
4
5
 Verfahren
Verfahren