|
Eingabe: G in CNF G = (N,T, P, S), deren Regeln von 1 bis p nummeriert sind, ein Eingabewort w = x1x2 · · · xn aus T* und
eine Parsematrix M.
Ausgabe: Linksparse für w (falls in L(G)) oder "Fehler".
Methode:
genLP(i,j,A) generiert den Linksparse für A=>+ xixi+1 · · · xi+j-1.
(Tij enthält A, falls der Linksparse existiert)
genLP(i,j,A) =
- Falls j=1 und A
 ai die Regel mit der Nummer m in P ist, dann gebe m aus. ai die Regel mit der Nummer m in P ist, dann gebe m aus.
Rekursionsanfang: Zur Ableitung des Teilwortes a wurde genau eine Regel genutzt.
- Falls j>1: k ist die kleinste Zahl zwischen 0 und j, so dass es A
 BC die m-te Regel ist,
Tik B und T(i+k)(j-k) C enthält.
Der Parse setzt sich zusammen aus m, das gefolgt wird von den Ergebnissen aus genLP(i,k,B), gefolgt von genLP(i+k,j-k,C). BC die m-te Regel ist,
Tik B und T(i+k)(j-k) C enthält.
Der Parse setzt sich zusammen aus m, das gefolgt wird von den Ergebnissen aus genLP(i,k,B), gefolgt von genLP(i+k,j-k,C).
Der Linksparse ergibt sich aus der Ableitung des Teilwortes.
Start mit genLP(1,n,S)
|
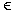 L(G) möchte man außerdem wissen, welche Ableitungen möglich sind.
Der folgende Algorithmus berechnet aus der gefüllten Dreiecksmatrix einen Linksparse.
L(G) möchte man außerdem wissen, welche Ableitungen möglich sind.
Der folgende Algorithmus berechnet aus der gefüllten Dreiecksmatrix einen Linksparse.
 YZ mit der Nummer m) wird expandiert.
Anschließend wird das erste Nichtterminal der rechten Regelseite (hier Y) weiter expandiert.
YZ mit der Nummer m) wird expandiert.
Anschließend wird das erste Nichtterminal der rechten Regelseite (hier Y) weiter expandiert. 1
2
3
4
5
1
2
3
4
5
 Üben
Üben