Suche Home Einstellungen Anmelden Hilfe

Schema eines Kellerautomaten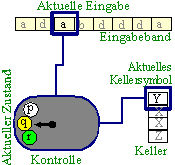 Ein KA in Graphendarstellung 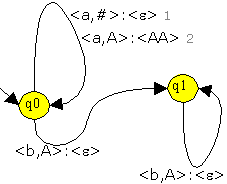Die Kantenbezeichnung bedeutet: <Eingabe,Kellersymbol>:<neue Kellersymbole>

Auch Kellerautomaten (KA) besitzen ein Eingabeband, dessen Zellen nur gelesen werden können. Genau wie beim EA wird das Eingabewort Zeichen für Zeichen gelesen, ohne dass Rücksprünge möglich sind. KA sind im Vergleich zu EA um einen Keller (stack) erweitert. In diesem können sie Hilfssymbole in unbegrenzter Anzahl zwischenspeichern. Allerdings kann nur auf die oberste Zelle des Kellers zugegriffen werden. Ebenso werden neue Elemente immer von oben auf bereits vorhandene Elemente in den Keller geschoben. Der Keller funktioniert nach dem Prinzip last-in-first-out. Es gibt zwei unterschiedliche aber äquivalente Konzeptionen von KA. Im ersten Konzept enthält der KA speziell ausgezeichnete Endzustände, die eine Teilmenge aller Zustände bilden. Hier wird die Analyse, wie erwartet, akzeptierend beendet, falls sich der KA am Wortende in einem Endzustand befindet. Die alternative Darstellung verzichtet auf die Definition von Endzuständen. Der Automat akzeptiert am Wortende, falls der Keller vollständig geleert wurde. Beim Übergang von einer Konfiguration in die Folgekonfiguration wird das aktuelle Eingabezeichen, das oberste Kellersymbol und der aktuelle Zustand berücksichtigt. Ein passender Übergang enthält den Folgezustand und die Hilfsymbole, die neu im Keller gespeichert werden sollen. Der Lesekopf verschiebt sich um eine Position (Ausnahme: ε-Übergänge: der Übergang erfolgt unabhängig von der Eingabe), und das bisherige oberste Kellersymbol wird entfernt. Auch der KA lässt sich dem EA ähnlich als Graph darstellen. Knoten bilden die Zustände und die Kanten die möglichen Übergänge zwischen den Zuständen. Die Kantenbeschriftung muss umfangreicher sein: <Eingabe,Kellersymbol>:<neue Kellersymbole>. Mit dem Keller steht dem KA bereits ein sehr mächtiges Hilfsmittel zur Verfügung. Allerdings bleiben Beschränkungen, da der Zugang zu den Kellerinformationen auf die oberste Zelle beschränkt ist. Er benötigt dadurch aber auch mehr Speicherplatz bei der Wortanalyse als ein EA. Durch den Keller kann die Anzahl der Rechenschritte erheblich anwachsen. So kann es passieren, dass wiederholt Übergänge allein den Kellerinhalt verändern, ohne ein Eingabezeichen zu verarbeiten. Der KA gibt zum Abschluss der Analyse nur aus, ob das Eingabewort zur von ihm akzeptierten Sprache gehört oder nicht. Eine Baumstruktur wie sie von Grammatiken bekannt ist, entsteht dabei nicht. Damit erfüllt ein solcher Automat nicht das zweite Ziel des Parsens.

Endliche Automaten 1   2   3   4   5   6   Turingmaschinen

Benutzer: Gast • Besitzer: matthias • Zuletzt geändert am: