Suche Home Einstellungen Anmelden Hilfe

1.2.2 Turingmaschinen

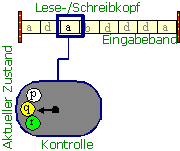
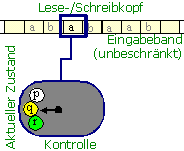
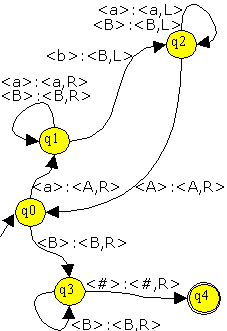
Schema einer TM Eine TM als Graph Die Kantenbezeichnung bedeutet: <Eingabe>:<neues Zellensymbol, Bewegungsrichtung>

TM besitzen ein Arbeitsband, dessen Zellen sowohl gelesen als auch beschrieben werden können. Das Arbeitsband ist in seiner Größe nicht begrenzt. In der Grundposition befindet sich der Lese-/Schreibkopf über dem ersten Buchstaben des Wortes. Er kann sich dann jedoch sowohl nach rechts als auch links bewegen. Rückspünge, mehrmaliges Lesen einer Zelle usw. sind möglich. Das Arbeitsband kann somit (Zwischen)-Ergebnisse in unbegrenzter Größe speichern. Auch eine Turingmaschine besitzt Zustände. Sie hält akzeptierend, wenn sie einen Endzustand erreicht. An welcher Stelle der Eingabe dabei der Lese-/Schreibkopf steht, ist nicht wichtig. Beim Übergang von einer Konfiguration in die nächste werden der aktuelle Zustand und das aktuelle Eingabezeichen betrachtet. Ist ein Übergang in der Kontrolle kodiert, so umfasst dieser drei Komponenten: den neuen Zustand, das Zeichen, das auf das Arbeitsband geschrieben werden soll, und die Richtung, in die sich der Lese-/Schreibkopf bewegen soll (z.B. L und R) Durch den unbegrenzten Arbeitsbereich ist eine TM sehr mächtig. Die TM ist ein Berechenbarkeitsmodell und jedes Problem, das überhaupt berechnet werden kann, kann dies durch die simplen Anweisungen einer TM. Die Unbegrenztheit stellt aber auch ein Problem dar: Man stelle sich vor, die TM bearbeitet ein Wort, das nicht zur von ihr akzeptierten Sprache gehört. Aufgrund ihres Wissens über die Sprache - kodiert in den Übergängen - wartet sie auf ein bestimmtes Eingabezeichen. So bewegt sich der Lese-/Schreibkopf immer weiter und weiter nach rechts. Obwohl das Wortende schon lange überschritten ist, bleibt sie auf der Suche nach diesem bestimmten Zeichen. Da das Arbeitsband in seiner Länge nicht beschränkt ist, sucht sie immer weiter ohne je anzuhalten.

Linear beschränkte Automaten

Schema eines LBA

Ein LBA ist eine beschränkte TM. Im Aufbau und Arbeitsweise entsprechen sie den TM. Allerdings besitzen sie ein in der Länge beschränktes Arbeitsband. Dieses ist auf die Länge des Eingabewortes begrenzt. Der Lese-/Schreibkopf eines LBA kann sich nicht über die erste und letzte Zelle des Eingabewortes hinausbewegen. Durch diese Beschränkung umgeht der LBA das Halteproblem der TM, er ist aber auch nicht so mächtig wie eine TM. Aber für die allermeisten Sprachprobleme reicht es. LBA und TM nutzen das Arbeitsband zur Speicherung von Zwischenergebnissen. Ältere Einträge werden im Verlauf der Analyse durch neuere überschrieben, weshalb am Ende der Analyse die Zwischenschritte nur unvollständig nachempfunden werden können. Das zellenweise Zugreifen auf Bandinhalte ist sehr ineffizient. So muss z.B. für das Kopieren eines Wortteils auf einen freien Bandbereich der Lese-/Schreibkopf ein Vielfaches der Wortlänge an Rechenschritten ausführen. Beim Halt liefert das Arbeitsband zwar eine Ausgabe, die Baumstruktur des Eingabewortes wurde jedoch nicht gefunden.

Kellerautomaten 1   2   3   4   5   6   Zusammenfassung

Benutzer: Gast • Besitzer: matthias • Zuletzt geändert am: