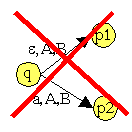
KA ohne Konflikte zwischen:
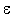 /nicht- /nicht-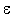 - Übergang - Übergang
nicht-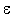 -/nicht- -/nicht-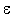 - Übergang - Übergang
|
Deterministische Kellerautomaten sind ähnlich wie nicht-deterministische aufgebaut.
Ein KA ist deterministisch, wenn die folgenden zwei Bedingungen erfüllt sind:
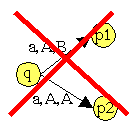
- Es tritt kein Konflikt zwischen einem
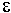 -move und einem nicht- -move und einem nicht-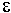 -move auf. -move auf.
Forderung: 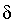 (q,a,Z) muss leer sein,
wenn (q,a,Z) muss leer sein,
wenn 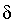 (q, (q,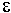 ,Z) nicht leer ist ,Z) nicht leer ist
- Es tritt kein Konflikt zwischen verschiedenen nicht-
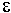 -moves auf. -moves auf.
Forderung: 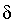 (q,a,Z) darf maximal 1 Element enthalten. (q,a,Z) darf maximal 1 Element enthalten.
Dies muss für alle q aus Q, alle a aus 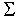 und alle Z aus und alle Z aus  erfüllt sein. erfüllt sein.
Nicht für jede Sprache, die mit einem Nicht-Deterministischen KA beschrieben werden kann,
lässt sich ein Deterministischer KA finden.
Ein Beispiel für eine Sprache, die nicht von einem deterministischen Kellerautomaten beschrieben werden kann, ist die Spiegelsprache.
In dieser Sprache besteht jedes Wort aus zwei Teilwörtern über einem 2-Elementigen Alphabet, z.B. {a,b}, wobei das zweite Teilwort eine exakte Spiegelung des ersten Teilwortes ist.
Der Automat kann nicht wissen, wann der gespiegelte Teil des Wortes anfängt, bevor er nicht das gesamte Wort gelesen hat.
Auch Palindrome haben diese Spiegeleigenschaft.
Palindrome können sowohl von vorn als auch von hinten gelesen werden.
Beispiele sind 'otto', 'nennen'. Aber auch ganze Sätze kann man konstruieren, wie z.B. 'Einsen essen es nie' (wobei die Leerzeichen nicht beachtet werden).
|


 1
2
3
4
5
6
1
2
3
4
5
6
 Übersicht: Sprachklassen
Übersicht: Sprachklassen