|
| |||||||||||
|
2.3.3 Greibach-Normalform (GNF): |
|
Ziel: Jede Regel hat die Form A | |
Ausgangspunkt: Eine Grammatik in Chomsky-Normalform enthält ausschließlich Regeln der Form1
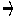 a und
A a und
A 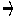 B C B C
Der erste Regeltyp entspricht bereits der GNF. Nur Regeln des zweiten Typs sind noch nicht im richtigen Format.
Terminalsymbole werden nun unweigerlich mit einer Regel des Typs 1 eingeführt. | |
|
Die ursprünglichen Regeln führen u.a. zu folgenden Teilbäumen:
|
Beispiel: Sei in einer Grammatik G folgende Regel:
Seien weiterhin die folgenden Regeln alle Regeln, in denen B das Nichtterminal der linken Regelseite ist (= alle "B-Regeln"):
Anstelle der 1. Regel führt man nun modifizierte Regeln ein. Diese entstehen, indem das B der rechten Regelseite (Regel 1) jeweils durch eine rechte Regelseite einer B-Regel ersetzt wird (Regel 2 und Regel 3). So erhält man die unten stehenden Regeln. Die generierte Sprache wird dadurch jedoch nicht verändert.
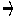 a C und a C und A 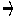 A B C A B C
Warum ist das möglich? Hier nun einige allgemeine Betrachtungen. Gegeben sei eine Grammatik G mit einer A-Regel A Für eine neue Grammatik G' entfernt man aus P die Regel A |
Greibach-Normalform
 1
2
3
4
5
6
1
2
3
4
5
6
 Weiteres Vorgehen
Weiteres Vorgehen
|
|