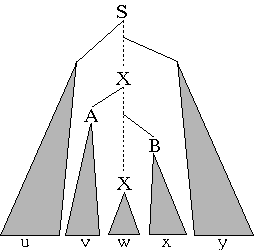
Auf dem längsten Pfad ist mindestens 1 Nichtterminal doppelt - hier mit X bezeichnet.
Diese Knoten sind dabei die ersten beiden doppelten vom Blatt aus gesehen.
Xoben überspannt einen Teilbaum der nicht größer als 2n sein kann (längster Pfad).
Der von Xoben überspannte Bereich der Eingabe wird durch t1 bezeichnet.
Der von Xunten überspannte Bereich der Eingabe wird durch t2 bezeichnet.
t1 lässt sich aufteilen in t3t2t4, wobei nicht sowohl t3 als auch t4 leer sein können,
da X durch eine Regel der Form X -> AB expandiert wurde. t2 ist dabei vollständig in einem Teilbaum von Xoben enthalten.
Es gilt X =>* t3Xt4 und X =>* t2. Daraus folgt jedoch X =>* t3it2t4i für beliebiges u und y.
t3=v, t2=w, t4=x;
Am konkreten Beispiel
|
Ebenso wie für reguläre Sprachen gibt es auch für kontextfreie Sprachen ein Schleifenlemma.
Ist eine Sprache kontextfrei, so genügt sie dem Schleifenlemma.
Das Schleifenlemma besagt, dass die Wörter kontextfreier Sprachen ab einer gewissen Länge so zerlegt werden können,
dass es zwei Teilwörter gibt, die in gleichem Maße vervielfältigt werden können.
| Für jede kontextfreie Sprache L gibt es eine Konstante n (aus dem Bereich der natürlichen Zahlen),
so dass sich jedes Wort z aus L, das mindestens so lang wie n ist, zerlegen lässt in z = uvwxy,
wobei gilt |vwx| =< n und |vx| >= 1,
und die Wörter uviwxiy (i ist eine natüliche Zahl) auch zu L gehören.
|
Für G in CNF: Sei n die Anzahl der Nichtterminalsymbole einer Grammatik in CNF und die Länge des Wortes 2n.
Ein Binärbaum mit 2n Blättern hat mindestens einen Pfad der Länge >= n.
Mit dem Pfad zum Blatt sogar eine Länge von mindestens n+1.
Mit dem Startsymbol liegen n+1 Nichtterminale auf dem Pfad, da n jedoch gerade die Anzahl der Nichtterminalsymbole in der Grammatik war,
kommt mindestens eine Variable doppelt vor ("Schubfachschluss").
An dieser Stelle wird aufgepumpt.
Diese Stelle findet man, indem man vom Terminalwort aus den längsten Pfad hin zur Wurzel verfolgt.
|

 1
2
3
4
5
6
1
2
3
4
5
6
 Anwendung des Schleifenlemma
Anwendung des Schleifenlemma