|
| |||||||||||
|
4.3.2 Reguläre Ausdrücke und Dycksprachen |
|
Reguläre Ausdrücke RA: RA lassen sich mit nur wenigen Basiskomponenten bilden. Die leere Menge, das leere Wort und jedes Zeichen aus dem Alpabet sind RA. Aus bestehenden RA lassen sich neue mittels Sternbildung, Verknüpfung (Konkatenation) und Vereinigung bilden.
Reguläre Ausdrücke sind ein Beschreibungsmittel für reguläre Sprachen. Sie stehen damit auf einer Stufe mit einseitig linearen Grammatiken und Endlichen Automaten. | ||||||||||||||||||||||
|
Schema für die Verarbeitung von Dycksprachen. Der Keller eines KA kann die Zeichen so speichern, dass sie korrekt ineinander geschachtelt sind. 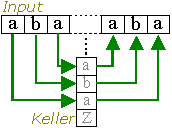
|
Dycksprachen Dn:
Dycksprachen sind Klammersprachen.
In den Wörtern einer Dycksprache wird jede öffnende Klammer auch wieder geschlossen.
Außerdem sind die Klammerpaare ineinander verschachtelt, d.h. es gibt keine Überkreuzungen.
Der Index n
Die Dycksprachen sind kontextfrei. Man kann das leicht nachvollziehen, indem man sich die Verarbeitung einer Dycksprache mit einem Kellerautomaten vorstellt: Jede öffnende Klammer wird im Keller abgelegt. Wird eine schließende Klammer eingelesen, so wird verglichen, ob sie zu der öffnenden Klammer im Keller passt. Diese Vorgehensweise verdeutlicht auch die Notwendigkeit von Schachtelungen. |
|
Arbeiten Sie mit dem JFLAP-Tool an einem Beispiel zur Schnittmengenbildung.
|
Abgeschlossenheit gegenüber Schnittmengenbildung: Die Abgeschlossenheit von kontextfreien Sprachen gegenüber der Schnittmengenbildung mit regulären Sprachen lässt sich am besten durch einen Automaten verdeutlichen.
und A = (QA, Σ, δA, p0, FM) ein Endlicher Automat, dann ergibt sich M' mit L(M') = L(M) ∩ L(A): M' = (QA x QM, Σ, ΓM, δ, [p0,q0], Z0, FA x FM) mit ([p',q'],Y) 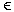 δ([p,q],a,X) δ([p,q],a,X)
für (q',Y) 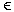 δM(q,a,X) und (p' δM(q,a,X) und (p' Bei der Verarbeitung eines Eingabewortes werden beide Automaten parallel abgelaufen. Befinden sich am Wortende beide Automaten in einem Endzustand, so wird das Wort akzeptiert. |
Prinzip
 1
2
3
4
5
6
1
2
3
4
5
6
 Homomorphismen
Homomorphismen
|
|