|
L = {wwR | w 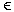 {a,b}* und wR ist das Spiegelbild von w} {a,b}* und wR ist das Spiegelbild von w}
Zu dieser Sprache gehören z.B. die Wörter: aabbaa, babaabab, aa und aabbaabbaa.
R = {a1  b1}*{a2 b1}*{a2  b2}* b2}*
R ∩ D2 sorgt für gleiche Anzahl von öffnenden und schließenden Klammern im Paar
und für die korrekte Schachtelung
| a |
a1 |
b1 |
a2 |
b2 |
|---|
| h(a) |
a |
b |
a |
b |
|
L = {wa|w| | w 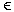 {a,b}*} {a,b}*}
Diese Sprache umfasst diejenigen Wörter, die im ersten Teil aus einer beliebigen Folge von a's und b's bestehen;
im zweiten Wortteil folgen soviele a's wie das erste Teilwort Zeichen hatte, also z.B.
abaa, bbbaaa, ababaaaa und aaaa.
R = {a1a2c1  b1b2c1}* c2* b1b2c1}* c2*
R muss mit D3 geschnitten werden, damit die 3 Klammerpaare ordentlich aufgebaut werden.
Es entsteht {a1a2c1  b1b2c1}n c2n b1b2c1}n c2n
Der Homomorphismus muss nun noch einiges im Ausdruck vereinfachen:
| a |
a1 |
a2 |
b1 |
b2 |
c1 |
c2 |
|---|
| h(a) |
a |
ε |
b |
ε |
ε |
a |
Dieses Beispiel verdeutlicht die Tilgung von Zeichen mittels Homomorphismus.
Im Regulären Ausdruck müssen immer Klammerpaare auftreten - also öffnende und zugehörige schließende Klammer.
Aber nicht immer werden alle Elemente auch in der Zielsprache gebraucht, wie in diesem Beispiel.
|
 1
2
3
4
5
6
1
2
3
4
5
6
 Kontextfreie Grammatiken und Kellerautomaten
Kontextfreie Grammatiken und Kellerautomaten