|
| |||||||||||
|
4.3.2 Homomorphismen |
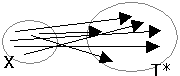
Der Homomorphismus ist eine Abbildung zwischen Mengen.
|
Der Homomorphismus ist eine Abbildung von einem Alphabet X1 in ein Alphabet X2. Auf diese Weise gibt es für jedes Wort in einer Sprache eine Entsprechung in einem anderen Alphabet. Das ist z.B. sinnvoll, um Sprachen besser miteinander zu vergleichen. Definition:
h: X1 → X2*
Bei der Anwendung eines Homomorphismus ändert man das Vokabular der Sprache nicht jedoch seine strukturellen Eigenschaften. | ||||||||||||
|
Beispiel: G1 = ({S,A,B,C},{a,b,c,d,e},P1,S) mit P1 = {S → ASA | ε, A→ bBb, B→ aCe, C→ dc }
So ist G2 = ({S,A,B,C},{ute,g,ta,n},P2,S) mit P2 = {S → ASA | ε, A→ gBg, B→ uteC, C→ nta } |
Abgeschlossenheit von kontextfreien Sprachen gegenüber Homomorphismen: Die Abgeschlossenheit gegenüber Homomorphismus lässt sich mittels der Konstruktion einer Grammatik gut zeigen.
Man kann eine kontextfreie Grammatik G2 konstruieren, so dass L(G2)=h(L(G1)). Sei G2 = (N,T,P2,S). A → w 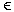 P1 ↔ A → w' P1 ↔ A → w' 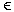 P2; P2;
w' ergibt sich aus w, indem alle Terminalsymbole a 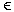 Σ durch h(a) ersetzt werden. Σ durch h(a) ersetzt werden.
|
RA und Dycksprachen
 1
2
3
4
5
6
1
2
3
4
5
6
 Beispiel
Beispiel
|
|