Gegeben einen NEA M=(Q,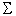 , ,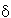 ,q0,F), ,q0,F),
so konstruiert man einen DEA M' mit L(M)=L(M').
Dabei ist Q' = 2Q (Potenzmenge),
q0' = {q0},
F' = {E | E ist eine Teilmenge von Q und enthält mindestens einen Zustand aus F},
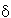 '(Z,a):= '(Z,a):=  [alle q aus Z] [alle q aus Z]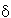 (q,a) (q,a)
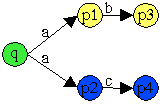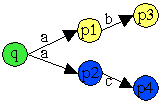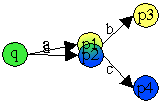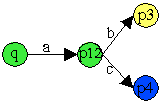
Abb. Verschmelzen von Zuständen.
Der NEA ist nur als Auschnitt gegeben, die Transformation ist nicht vollständig.
|
|
Effizient sind Systeme dann, wenn sie deterministisch arbeiten.
Ein deterministisches Verfahren braucht keine Buchführung darüber, welche weiteren Wege
es an jedem Punkt hätte einschlagen können.
Sobald im deterministischen System eine Konfiguration auftritt, die nicht verarbeitet werden kann, ist die Analyse zu beenden.
An dieser Stelle sind alle Möglichkeiten abgearbeitet.
Im nicht-deterministischen Fall müssten an so einem Punkt Entscheidungen rückgängig gemacht und andere Möglichkeiten verfolgt werden.
Für EA kann man zeigen, dass DEA und NEA die gleiche Stärke aufweisen, d.h. man kann einen NEA in einen DEA überführen.
Beispiel
MErgänzung = ({q0,q1,q2,q3}, {GBu,KBu,Z,(,)},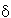 ,q0,{q0,q1}) ,q0,{q0,q1})
GBu steht für einen Großbuchstaben, KBu für einen Kleinbuchstaben und Z für eine Ziffer
|
Tabelle 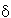 -Übergänge: -Übergänge:
| GBu | KBu | Z | ( | ) |
|---|
| q0 | {q1,q2} | | | | |
| q1 | | {q1} | | | |
| q2 | | {q2} | | {q3} | |
| q3 | | | {q3} | | {q0} |
|
Dieser Automat akzeptiert eine beliebige Anzahl von 'Bezeichner (Zahl)'; am Ende kann ein weiterer 'Bezeichner' folgen.
Ersetzt man GBu und KBu durch entsprechende Buchstaben, so gehört zur Sprache z.B. Potsdam (129000) Maastricht (1992) Thesenanschlag (1513).
Aus diesem NEA kann nach dem Verfahren zur Umwandlung ein DEA konstruiert werden.
Zur Übergangstabelle des DEA
|
Der DEA zu einem NEA kann sehr
unübersichtlich sein. So wird allein die
Zustandsmenge potenziert. Der entstehende DEA kann jedoch auch Zustände enthalten, die nicht mehr vom Startzustand aus erreichbar sind
oder von denen kein Endzustand erreichbar ist.
Ein solcher Automat lässt sich reduzieren, wie am Beispiel gezeigt wird.
Der kleinste zu einem gegebenen EA äquivalente Automat wird Minimalautomat genannt.
|
 Minimalautomat
Minimalautomat