|
Ein einfaches Beispiel verdeutlicht die Nicht-Erreichbarkeit
von Zuständen.
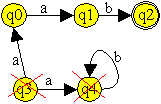
Eine Reduktion des EA um die nutzlosen Zustände
vereinfacht die meisten Automaten bereits erheblich. |
|
Welche Komponenten eines Automaten können minimiert werden?
Die Komplexität eines EA hängt von der Anzahl der Zustände
und von der Anzahl der Übergänge ab. Eine Reduktion wird also
genau dort ansetzen.
Es leuchtet ein, dass alle nicht erreichbaren Zustände ohne
Konsequenzen entfernt werden können. Zustände, die vom Startzustand
aus durch keine Folge von Übergängen erreicht werden, haben keinen
Einfluss auf die Analyse. Sie sind nutzlos.
Solche Zustände können z.B. durch eine Suche im Graphen gefunden
werden (Überlegen Sie, wie das im Detail ablaufen könnte!). Mit
den Zuständen verschwinden auch die an diese Zustände geknüpften
Übergänge.
Formal: Ein Zustand q ist nicht erreichbar, wenn es keinen Eingabestring
x gibt, so dass (q0,x) |-* (q,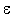 ). ).
Ist eine weitere Minimierung des EA möglich?
Folgende Situation: Bei der Analyse zweier Wörter v und w möge
"unterwegs" jeweils ein Zustand q1 bzw. q2 erreicht werden. Ab diesem Punkt
möge die Analyse für den Rest der beiden Wörter genau gleich
ablaufen; wir können also Zerlegungen von v=xu und w=yu finden, wobei
x bzw. y diejenigen Teilwörter sind, die bis zum Erreichen der Zustände
q1 bzw. q2 abgearbeitet wurden.
Wenn nach Erreichen verschiedener Zustände keine Unterschiede
mehr in der Analyse von Wörtern auftreten, so spielt es demnach keine
Rolle, über welchen Zustand die Analyse gelaufen ist. Die Zustände
q1 und q2 verhalten sich funktional identisch, realisieren also die gleiche
Funktion zumindest für die gedachten Wörter. Man nennt q1 und
q2 äquivalent. Besitzt ein Automat zwei äquivalente Zustände,
so können diese verschmolzen und der Automat verkleinert werden.
Im Folgenden wird ein allgemeines Verfahren vorgestellt, dass alle Paare
solcher äquivalenten (verschmelzbaren) Zustände
eines DEA ausgibt. |
 1
2
3
4
5
6
1
2
3
4
5
6
 Äquivalenzklassen
Äquivalenzklassen