Suche Home Einstellungen Anmelden Hilfe

Minimierung 3: Äquivalenzklassen

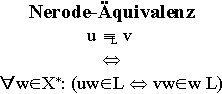
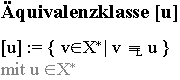
Zwei Wörter über einem Alphabet X heißen äquivalent, wenn sie das gleiche Verhalten bei der Verlängerung um Teilwörter aus X* aufweisen. Die entstehenden Wörter sind entweder beides Wörter oder beides Nicht-Wörter. Die Nerodeäquivalenz ist eine reflexive, symmetrische und transitive Relation. Eine Äquivalenzklasse umfasst alle äquivalenten Wörter über einem Alphabet (bezüglich einer Sprache) und wird durch einen beliebigen Repräsentanten bezeichnet.  Die Größe einer Menge von Äquivalenzklassen wird mit Index bezeichnet.

Das Konzept der verschmelzbaren Zustände entspricht nun genau dem Konzept der Äquivalenzklassen. Der Begriff der Äquivalenz besagt, dass zwei Wörter das gleiche funktionale Verhalten aufweisen.  Eine typische Quelle für Äquivalenzklassen sind Rekursionen. Rekursionen können einmal oder mehrmals durchlaufen werden oder gar nicht. Ob ein Wort entsteht oder nicht, hängt jedoch nur von denjenigen Teilwörtern ab, die dem Ende der Rekursion angehangen werden. Beispiel: Tags in XML sind immer zweiteilig und müssen korrekt in einander verschachtelt sein. Alle folgenden Teilwörter gehören zu einer Äquivalenzklasse. <p> Absatz </p> <p><b><i> fett und kursiv </i></b> ... </p>  <p><b><i> fett und kursiv </i></b> ... <b> fett </b> ... </p>  Beispiel: Auch fürs Deutsche lassen sich Äquivalenzklassen finden. Die Tabelle zeigt einige Teilsätze, die einer Klasse angehören. Alle könnten durch die Teilsätze der 3. Tabellenspalte verlängert werden und bilden korrekte Sätze. Eine Verlängerung um bspw. "Ärger großer" führt in keinem Fall zu einem korrekt gebildeten Satz.  Äquivalente Teilsätze im Deutschen     "der große, rote Papagei"  "die alte verschrumpelte Hexe" "der Mann, der sich immer wegen der Lärmbelästigung aufregt,"  +  "plustert sich auf" "sitzt auf dem Stuhl" "fährt Auto" "ißt Spaghetti" Hinweis: Die entstehenden Sätze sind alle syntaktisch wohlgeformt, es kann jedoch zu semantischen Anomalien kommen, da z.B. Papageien nicht Auto fahren können und Männer nicht einfach im Zimmer fliegend Kreise ziehen. Aufgabe: Finden Sie für weitere Sprachen Äquivalenzklassen. Beschreiben Sie die Äquivalenzklasse von ["heute ist"].

Reduzierung 1   2   3   4  5   6 Verfahren

Benutzer: Gast • Besitzer: senn • Zuletzt geändert am: